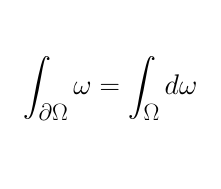Concretization: Conditional Probability and Expectation

Background required: basic measure theory and probability theory ($\sigma$-fields, measurable sets and functions, probability measures, random variables).

In modern probability theory, we don't define conditional probability with the usual formula: $$ P(A | B) = \frac{P(A \cap B)}{P(B)} $$

Instead we use a much more abstract formulation where we condition on an entire $\sigma$-field. This is much more general but also very far from the basic definition, and I found it very difficult to find an explanation of how to obtain the basic definition from the general one (eventually I found it in one of the exercises in Billingsley).

General Conditional Expectation

At the intro level, the conditional expectation of a random variable $X$ on a random variable $Y$ is defined as: $$ E[X | Y=y] = \sum_x x P(X=x | Y=y) $$ This is nice and intuitive: we just take the formula for expectation and change the probability to a conditional probability.

General conditional expectation is not quite so nice. We don't even construct it: we use the Radon-Nikodym theorem to prove that a random variable with a certain property must exist and be unique, and define that random variable as the conditional expectation.

We define the conditional expectation of a random variable $X$ on a $\sigma$-field $\mathcal{G}$ as a random variable $E[X | \mathcal{G}]$ that satisfies: $$ \int_G E[X | \mathcal{G}] dP = \int_G X dP $$ for all $\mathcal{G}$ measurable sets $G$. We also require that $E[X | \mathcal{G}]$ be $\mathcal{G}$-measurable.

First, not that $E[X | \mathcal{G}]$ isn't* being defined as an expectation operator being applied to the random variable $X$. $E[X | \mathcal{G}]$ defines a *single random variable with a weird notation.

Some intution: Suppose we're flipping a coin twice, and $X$ is the sum of the flips (heads is 1 and tails is 0). We want to condition $X$ on the first flip. With out new definition, we need to build a $\sigma$-field that only sees the first flip, i.e. one that cannot distinguish between the events $TH$ and $TT$ (and $HH$ and $HT$). If we think in terms of conditioning on a random variable, the groups would be "all events that have the same value for the random variable we're conditioning on". So we define $\mathcal{G}$ as: $$ \mathcal{G} := \{\emptyset, \{TH, TT\}, \{HH, HT\}, \Omega\} $$

Note that $X$ isn't $\mathcal{G}$-measurable. The pre-image of $0$ under $X$ is $TT$: that's not a measurable set in $\mathcal{G}$. That's why we require $E[X | \mathcal{G}]$ to be $\mathcal{G}$-measurable: we construct $\mathcal{G}$ in a constrained way, grouping all the events that are the same under the condition together. Our original variable won't be measurable against these because it sees the individual events, not the groups, so we have to make a new variable that only sees the groups.

The integral condition looks weird, but really it's just demanding that our conditional expectations satisfy the law of total expectation.

For some alternate intuition: if $X$ is in $L_2$, then $E[X | \mathcal{G}]$ is the Hilbert space projection of $X$ onto $\mathcal{G}$.

Conditional probability on a $\sigma$ - field

Getting conditional probability out of this definition is very easy: the conditional probability of an event $A$ on a $\sigma$-field $\mathcal{G}$ is the conditional expectation of its indicator variable: $$ P(A | \mathcal{G}) := E[I_A | \mathcal{G}] $$ (The indicator variable $I_A$ is $1$ when $A$ occurs and $0$ otherwise. The unconditional expectation of $I_A$ is $P(A)$, and we generalize that property to conditional probability).

Returning to our coin flip example, suppose we want to compute the probability the second flip is heads conditional on the first flip. Let's compute the integrals:

$$ \begin{align} \int_{\{TH, TT\}} E[I\_A | \mathcal{G}] dP &= \int_{\{TH, TT\}} I_A dP \\ &= I_A(TT) * 0.25 + I_A(TH) * 0.25 \\ &= 0.25 \end{align} $$ and of course $$ \int_{\{TH, TT\}} E[I_A | \mathcal{G}] dP = E[I_A | \mathcal{G}] (TT)P(TT) + E[I_A | \mathcal{G}] (TH)P(TH) $$ We know that $E[I_A | \mathcal{G}] (TH) = E[I_A | \mathcal{G}] (TT)$ (since it's $\mathcal{G}$-measurable). Define their value as $x$. So we have: $$ \begin{align} x P(TT) + x P(TH) &= \int_{\{TH, TT\}} E[I_A | \mathcal{G}] dP\\ 0.25x + 0.25x &= 0.25\\\\ x &= 0.5 \end{align} $$ which is the answer we expect (of course a similar calculation applies to $HH$ and $HT$)

Conditioning on an event

Now we want to condition on a single event $B$. To do this, we condition on the $\sigma$-field generated by the event, i.e. the $\sigma$-field generated by $\{B, B^C\}$. Now let $\omega$ be any element of $B$. Then the conditional expectation of a $X$ on $B$ is $E[X | \sigma(\{B, B^c\})]$ evaluated at $\omega$.

In our coin flip example: if we make $B$ the event that the first flip is tails (so $B = \{TT, TH\}$) we can condition on $B$ by taking $E[X | \mathcal{G}]$ and evaluating it at either $TT$ or $TH$ (the answer will be the same either way, since $E[X | \mathcal{G}]$ is $\mathcal{G}$-measurable).

Probability conditional on an event

Finally we arrive at the familiar $P(A | B)$. By our previous definitions, this is: $$ P(A | B) = E[I_A | \sigma(\{B, B^C\})] (\omega) $$ for some $\omega \in B$.

Let's derive the familiar $P(A | B) = P(A \cap B) / P(B)$ formula from this.

Suppose we're working entirely with discrete probabilities. Because $E[I_A | \sigma(\{B, B^C\})$ is measurable against $E[I_A | \sigma(\{B, B^C\})$, it must be constant on $B$. Call this value $c$. Since it's constant, we know that the integral over $B$ is just the constant times the probability of $B$: $$ \int_B E[I_A | \sigma(\{B, B^C\}) dP = c \int_B dP = c P(B) $$ We also know that $\int_B E[I_A | \sigma(\{B, B^C\}) dP = \int_B I_A dP$, by the definition of conditional expectation. But the right hand side is simply $P(A \cap B)$, so we have: $$ \begin{align} c P(B) &= P(A \cap B) \\\\ c &= \frac{P(A \cap B)}{P(B)}\\\\ E[I_A | \sigma(\{B, B^C\})] &= \frac{P(A \cap B)}{P(B)}\\\\ P(A | B) &= \frac{P(A \cap B)}{P(B)} \end{align} $$